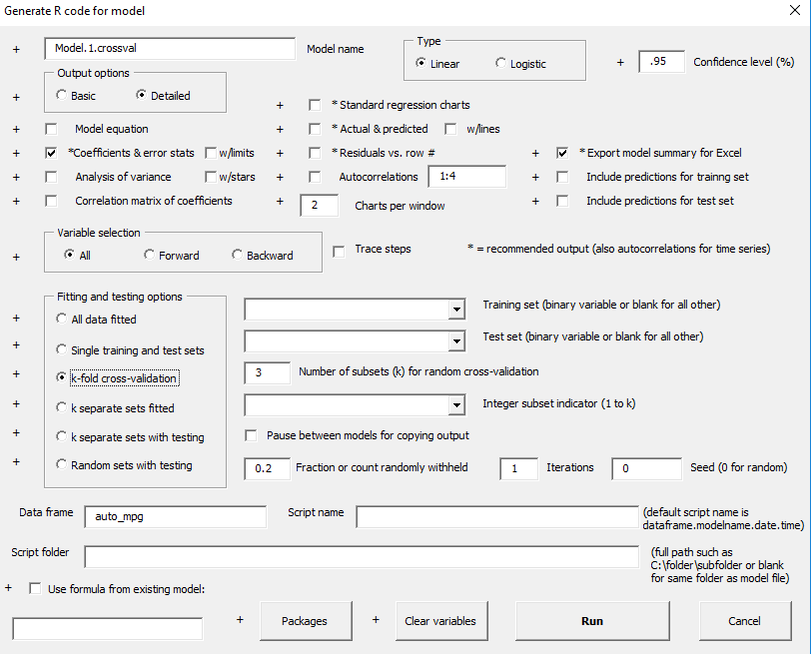
k-fold cross-validation
Some of the other fitting and testing options allow many models to be fitted at once with output that includes customized model comparison tables. One of these options is is k-fold cross-validation, which is commonly used as a test against overfitting the data. In this method, the data set is broken up randomly into k subsets of equal size (as nearly as possible), and k models are fitted. In each of them k-1 subsets are used for training and the remaining subset used for testing. Ideally the training and test error statistics should be very similar when averaged over the folds.
You can either choose randomly selected folds or preselected folds determined by an integer variables with values 1 through k. Here's a demonstration of 3-fold cross-validation with randomly chosen folds:
Some of the other fitting and testing options allow many models to be fitted at once with output that includes customized model comparison tables. One of these options is is k-fold cross-validation, which is commonly used as a test against overfitting the data. In this method, the data set is broken up randomly into k subsets of equal size (as nearly as possible), and k models are fitted. In each of them k-1 subsets are used for training and the remaining subset used for testing. Ideally the training and test error statistics should be very similar when averaged over the folds.
You can either choose randomly selected folds or preselected folds determined by an integer variables with values 1 through k. Here's a demonstration of 3-fold cross-validation with randomly chosen folds:
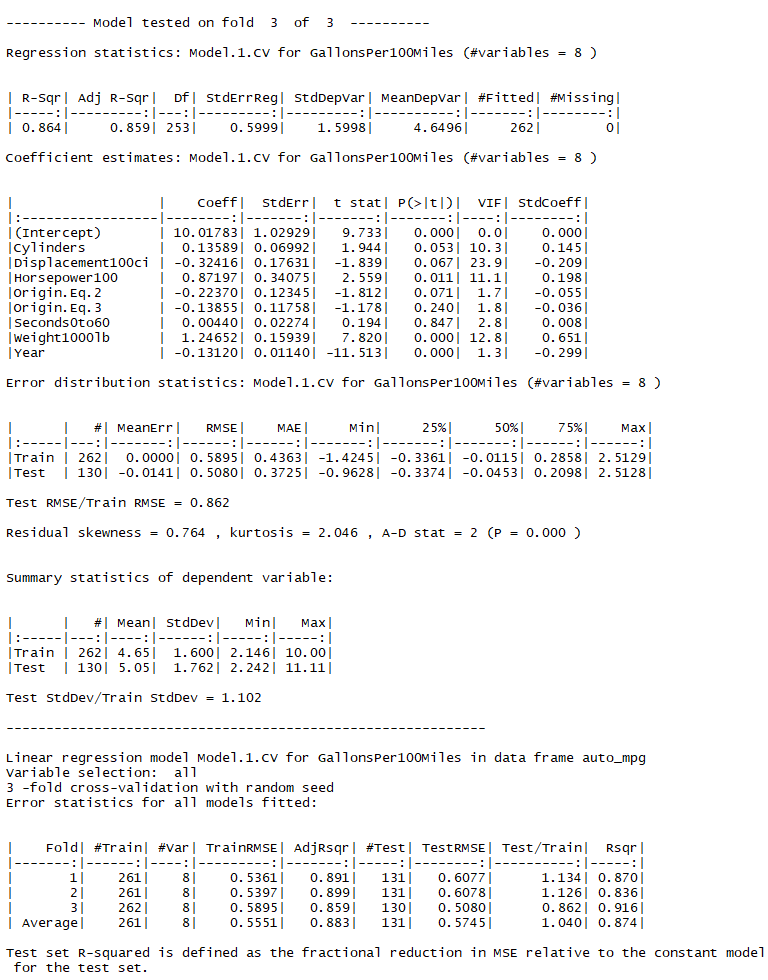
When the line of code for running this model is pasted and executed at the command prompt in RStudio, a lot of output is produced: complete results for the models for all 3 folds. Here is what the output looks like at the bottom, with the results for fold 3 showing. As in the case of the model fitted to all data (illustrated in the video), the displacement variable has a huge variance inflation factor and its coefficient has a counterintuitive negative sign, suggesting that it ought to be removed on grounds of multicollinearity. If you try to replicate this example, your results will differ because of the randomization of the folds.
At the very bottom is a summary table in which goodness-of-fit statistics are separately reported for the training and test sets for all of the folds, as well as their averages over the folds. The ratio of RMSE's between test and training sets is also shown for reference. Here the RMSE's in the test sets were about 4% larger on average than those in the training sets, although the ratio varied significantly from one fold to another. In particular, the test set RMSE for fold 3 was much lower than the training set RMSE. This variability is noteworthy (perhaps even surprising), and it is not seen in the default cross-validation output produced in R which shows only the averages.
The individual model worksheets can be exported back to Excel along with the summary table. The "Import R" tool on the RegressIt menu will place the results on separate worksheets, nicely formatted. Here's the Excel version of the summary table for this set of models:
The individual model worksheets can be exported back to Excel along with the summary table. The "Import R" tool on the RegressIt menu will place the results on separate worksheets, nicely formatted. Here's the Excel version of the summary table for this set of models: